1.2　波動方程式

  1. 体積弾性率


    2. 空気中の音波は、その圧力変動が早いので断熱変化と考えられる。従って、はじめ圧力Ｐ０、体積Ｖ０の気体が音圧ｐにより（Ｐ０＋ｐ）、体積が（Ｖ０＋ΔＶ）になったとすると定積比熱と定圧比熱の比をγ（空気では、1.4）として、
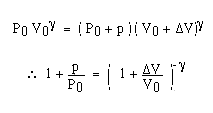    いま右辺をTaylor展開し(ΔＶ/Ｖ０)が小さいため、２次以下の微小量を無視すれば
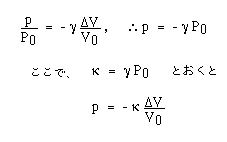    を得る。すなわち音圧は体積変化に比例し、その比例定数κを体積弾性率とよぶ。

  2. 波動方程式（一次元）


    3. 音圧に関する波動方程式は、連続の式の両辺をtで２階微分してξを消去すると、
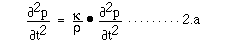    となる。また、運動の式の両辺をxで微分してξを消去すると、
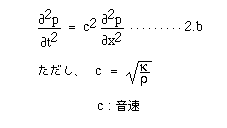    となる。同様にｐを消去すれば、ξに関する波動方程式が全く同じ形で得られる。ここで、新しい関数、速度ポテンシャルを下に示した関形式
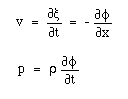    によって定義すると、これと基礎式である連続の式を用いて
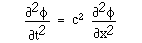    が得られ、音圧に関する方程式　2.ａ，2.ｂ　と全く同じ形になる。
    もし、音波が時間的に単弾振動していると、その関数形は角振動数をωとしてｅｊωｔを含み、
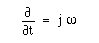    となるから
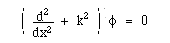    ただし、
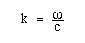    と表すことができ、ｋを波長定数または、波数(wave number)とよぶ。

  3. 波動方程式（三次元）


    4. 平面波の場合は１次元の場合と全く同様な考え方で媒質流体の連続の式から導くことができる。 ここでＬａｐｌａｃｅの微分演算子
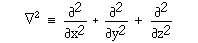    を用いれば
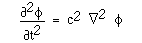    また音波が単弦波動であると、fは時間関数としてｅｊωｔをもつから、簡単に
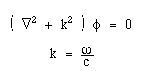    と表わすことができる。